Description
In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a/, \, or blank space. These characters divide the square into contiguous regions.
(Note that backslash characters are escaped, so a \ is represented as “\“.)
Return the number of regions.
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。
(请注意,反斜杠字符是转义的,因此 \ 用 “\“ 表示。)。
题目链接:https://leetcode.com/problems/regions-cut-by-slashes/
Difficulty: medium
Example 1:
Input:
[
" /",
"/ "
]
Output: 2
Explanation: The 2x2 grid is as follows:
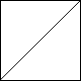
Example 2:
Input:
[
" /",
" "
]
Output: 1
Explanation: The 2x2 grid is as follows:
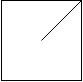
Example 3:
Input:
[
"\\/",
"/\\"
]
Output: 4
Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)
The 2x2 grid is as follows:
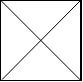
Example 4:
Input:
[
"/\\",
"\\/"
]
Output: 5
Explanation: (Recall that because \ characters are escaped, "/\\" refers to /\, and "\\/" refers to \/.)
The 2x2 grid is as follows:
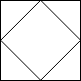
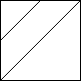
Example 5:
Input:
[
"//",
"/ "
]
Output: 3
Explanation: The 2x2 grid is as follows:
Note:
- 1 <= grid.length == grid[0].length <= 30
- grid[i][j] is either ‘/‘, ‘\’, or ‘ ‘.
分析
- updating(Solution)
参考代码
class DSU:
def __init__(self, N):
self.p = range(N)
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, x, y):
xr = self.find(x)
yr = self.find(y)
self.p[xr] = yr
class Solution(object):
def regionsBySlashes(self, grid):
N = len(grid)
dsu = DSU(4 * N * N)
for r, row in enumerate(grid):
for c, val in enumerate(row):
root = 4 * (r*N + c)
if val in '/ ':
dsu.union(root + 0, root + 1)
dsu.union(root + 2, root + 3)
if val in '\ ':
dsu.union(root + 0, root + 2)
dsu.union(root + 1, root + 3)
# north/south
if r+1 < N: dsu.union(root + 3, (root+4*N) + 0)
if r-1 >= 0: dsu.union(root + 0, (root-4*N) + 3)
# east/west
if c+1 < N: dsu.union(root + 2, (root+4) + 1)
if c-1 >= 0: dsu.union(root + 1, (root-4) + 2)
return sum(dsu.find(x) == x for x in xrange(4*N*N))